El modelo más popular para comprender una Epidemia se llama SIR, que
establece una relación entre los tres factores: Susceptibles, Infectados
y Recuperados, y que nos permite entender conceptos como el
aplanamiento de la curva de contagios.
El modelo esta dado por las Ecuaciones Diferenciales siguientes:
Hay dos condiciones en este modelo:
Digamos que empezamos con un 1% de la población infectada, con un 90% de ser contagiado, entonces observemos la curva azul, es el numero de casos de Infectados, como se ve, para un parámetro 𝛽 del 0.9, que significa un día normal, con montones de personas en la calle, tendremos que el 70% de la población se contagiara, y con un promedio de muertes del 4% del Coronavirus, entonces esa proporción de la población infectada morirá, entre menos infectados, menos muertes, así de simple.
Con 𝛽 = 0.9 Un alto nivel de personas susceptibles
Ahora bien, si se aplica una distancia adecuada y las personas se mantienen en casa, el factor 𝛽 disminuye:
Con 𝛽 = 0.4
Solo tendríamos el 45% infectados
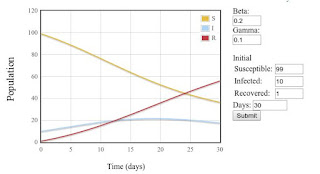
Con 𝛽 = 0.2
Solo tendríamos el 20% infectados
Como se ve, entre menor sea 𝛽, menos altura tiene la curva, menos muertes.
A eso se le llama aplanar la curva, y como se ve, 𝛽 depende de la distancia social, entre menos contagios, menos muertos, y si aceptamos que el virus se vuelve no mortal en un mes, entonces, por eso es importante mantener las medidas de estar en casa.
Entre menor sea la curva, menos pacientes necesitan ser hospitalizados, lo que implica menos carga de trabajo al personal médico y menos gasto social, es muy importante mantenerse en casa, por tí, por tú familia y por tú sociedad.
Los cálculos los hice calculando una mortalidad del 4%, que es la reportada hasta el momento, esperemos que en México no sea tan alta.
Existen otros Modelos, pero son más complejos y no son tan populares, en que se incluyen la cantidad de muertos, que los recuperados no se vuelvan inmunes y otros factores.
Si deseas revisar los números y hacer tú propio modelo, te dejo el enlace del simulador de la Universidad de Arizona:
http://www.public.asu.edu/~hnesse/classes/sir.html?Alpha=0.4&Beta=0.1&initialS=99&initialI=10&initialR=1&iters=30
Este artículo originalmente fue publicado en el Blog de mi Universidad.
El modelo esta dado por las Ecuaciones Diferenciales siguientes:
Hay dos condiciones en este modelo:
- No se toma en consideración el numero de muertos
- Existe un periodo de adaptación al virus, esto es, los Recuperados desarrollan inmunidad y la transmiten a otras personas, con lo cual, el virus deja de ser mortal.
Digamos que empezamos con un 1% de la población infectada, con un 90% de ser contagiado, entonces observemos la curva azul, es el numero de casos de Infectados, como se ve, para un parámetro 𝛽 del 0.9, que significa un día normal, con montones de personas en la calle, tendremos que el 70% de la población se contagiara, y con un promedio de muertes del 4% del Coronavirus, entonces esa proporción de la población infectada morirá, entre menos infectados, menos muertes, así de simple.
Con 𝛽 = 0.9 Un alto nivel de personas susceptibles
Ahora bien, si se aplica una distancia adecuada y las personas se mantienen en casa, el factor 𝛽 disminuye:
Con 𝛽 = 0.4
Solo tendríamos el 45% infectados
Con 𝛽 = 0.2
Solo tendríamos el 20% infectados
Como se ve, entre menor sea 𝛽, menos altura tiene la curva, menos muertes.
A eso se le llama aplanar la curva, y como se ve, 𝛽 depende de la distancia social, entre menos contagios, menos muertos, y si aceptamos que el virus se vuelve no mortal en un mes, entonces, por eso es importante mantener las medidas de estar en casa.
Entre menor sea la curva, menos pacientes necesitan ser hospitalizados, lo que implica menos carga de trabajo al personal médico y menos gasto social, es muy importante mantenerse en casa, por tí, por tú familia y por tú sociedad.
Los cálculos los hice calculando una mortalidad del 4%, que es la reportada hasta el momento, esperemos que en México no sea tan alta.
Existen otros Modelos, pero son más complejos y no son tan populares, en que se incluyen la cantidad de muertos, que los recuperados no se vuelvan inmunes y otros factores.
Si deseas revisar los números y hacer tú propio modelo, te dejo el enlace del simulador de la Universidad de Arizona:
http://www.public.asu.edu/~hnesse/classes/sir.html?Alpha=0.4&Beta=0.1&initialS=99&initialI=10&initialR=1&iters=30
Este artículo originalmente fue publicado en el Blog de mi Universidad.